前置知识
存图方式（邻接表，邻接矩阵）,图的遍历（dfs，bfs）
引入
我们举个例子吧： 有一个毒瘤水管工，他会造水管，有一天他造了一个水管网络，就像一个图。其中有一个点只有出边，就是源点（起点），还有一个点只有入边，是汇点（终点）。
点之间有一些管子，管子 \(i\) 在一个单位时间内能流 \(c_i\) 的水，现在毒瘤水管工想知道，他的水管在一个单位时间内，从源点最多能运多少水到汇点。
概念
- 源点：起点，一般用s表示；
- 汇点：终点，一般用t表示；
- 残余网络：进行增广后剩余的网络；
- 増广： > 増广就是在残余网络中寻找从源点到汇点的可行路径（増广路），并将该路径上的所有边的容量减去路径中的最小容量，形成新的残余网络，人话就是找一条能走的路，看看这条路上最窄的水管是那条，然后让最窄的水管满载运行。 例如：
![]()
如果当前有这样一个残余网络，那么 \(s\rightarrow4\rightarrow1\rightarrow t\) 就是一条増广路，最小容量是4，进行増广过后就形成了这样一张图： ![]()
如何寻找増广路？直接dfs即可。 - 反向边： > 有时候，増广的时会出现假的答案，例如还是那个图：
![]()
有 \(s\rightarrow4\rightarrow1\rightarrow t\) 和 \(s\rightarrow1\rightarrow t\) 两条増广路，万一程序选错了怎么办？ 这时就要请出反向边了。 每次増广的时候，在残余网络上逆着増广路径建容量与増广路径容量相等的反向边，比如刚才那张图，就顺着\(t\rightarrow1\rightarrow4\rightarrow s\)建容量为4的边。如果接下来増广时走过了反向边，就相当于把原来的増广撤回去了。 这就相当于给了程序一个反悔的机会。
朴素算法
- 増广
- 沿着増广路径建反向边
- 如果源点与汇点依然连通，回到1
Dinic优化
Dinic的优化就是用bfs建立了由s开始的一个分层图，每次寻找増广路时必须让边上的层数严格递增，就可以确保每一步都离汇点近了一些这样就不会陷入毒瘤数据卡成的死循环，比如这样的著名毒瘤数据：
![]()
在这个数据中，如果用朴素算法，就会让中间容量为1的边上下抖动抽搐，等到他抽了999次的时候才把上面和下面的999减没。如果用Dinic，则不会走中间的边，因为层数都是1。所以两次直接求出999+999。
![]()
代码
朴素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include "bits/stdc++.h"
using namespace std;
const long long N=10010,inf=0x3f3f3f3f3f3f3f3f;
struct node{
long long v,c,nxt;
}e[N<<1];
long long tot=1,h[N];
void adde(long long u,long long v,long long c){
e[++tot].v=v;
e[tot].c=c;
e[tot].nxt=h[u];
h[u]=tot;
}
long long n,m,ans,vis[N];
long long path(long long u,long long f){
if(vis[u])return 0;
vis[u]=true;
if(u==n)return f;
for(long long i=h[u];i;i=e[i].nxt){
long long v=e[i].v;
if(e[i].c){
long long fv=path(v,min(f,e[i].c));
if(fv){
e[i].c-=fv;
e[i^1].c+=fv;
return fv;
}
}
}
return 0;
}
void solve(){
long long d=0;
while(d=path(1,inf)){
ans+=d;
memset(vis,0,sizeof(vis));
}
}
int main(){
cin>>n>>m;
for(long long i=1;i<=m;i++){
long long u,v,c;
cin>>u>>v>>c;
adde(u,v,c);
adde(v,u,0);
}
solve();
cout<<ans<<endl;
return 0;
}
|
带优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include "iostream"
#include "cstring"
#include "queue"
using namespace std;
const int maxn=1e6+5;
const int INF=9999999;
int s,t,tot,n,m;
struct node{
int next;
int v;
int c;
}e[maxn];
int h[maxn],q[maxn],deth[maxn];
void add(int u,int v,int c){
e[tot].v=v;
e[tot].next=h[u];
e[tot].c=c;
h[u]=tot++;
}
int bfs(){
memset(deth,0,sizeof(deth));
queue<int> q;
while(!q.empty())q.pop();
deth[s]=1;
q.push(s);
do{
int u=q.front();
q.pop();
for(int i=h[u];i;i=e[i].next){
if(e[i].c>0&&deth[e[i].v]==0){
deth[e[i].v]=deth[u]+1;
q.push(e[i].v);
}
}
}
while(!q.empty());
if(deth[t]!=0)
return 1;
else return 0;
}
int dfs(int u,int dist)
{
if(u==t)return dist;
for(int i=h[u];i;i=e[i].next){
if((deth[e[i].v]==deth[u]+1)&&(e[i].c!=0)){
int di=dfs(e[i].v,min(dist,e[i].c));
if(di>0){
e[i].c-=di;
e[i^1].c+=di;
return di;
}
}
}
return 0;
}
int dinic(){
int ans=0;
while(bfs()){
while(int di=dfs(s,INF)){
ans+=di;
}
}
return ans;
}
int main(){
cin>>n>>m>>s>>t;
int x,y,z;
for(int i=0;i<m;i++){
cin>>x>>y>>z;
add(x,y,z);
add(y,x,0);
}
cout<<dinic()<<endl;
return 0;
}
|
我踩的坑
注意当实现朴素算法时，代码中的 dfs 不能回溯，只需要一条路走到底。
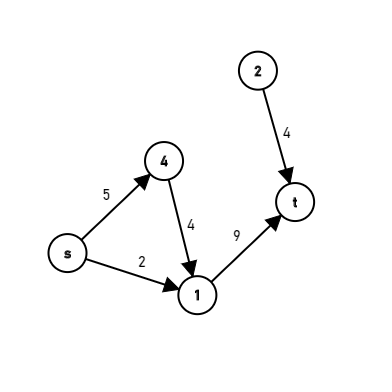如果当前有这样一个残余网络，那么 
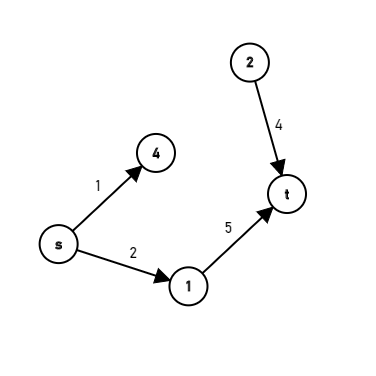如何寻找増广路？直接dfs即可。
